Московский
физико-технический институт (Государственный университет)
Факультет физической и квантовой электроники
Кафедра твердотельной электроники и радиофизики
Методическое дополнение к Лабораторной работе №1
«Затухание акустических волн в кристаллах»
Составил профессор Г. Д. Мансфельд
г. Москва 2006 г.
Недостатки эхо - метода
Применения методов акустоэлектроники для исследования упругих свойств материалов известны довольно давно. Среди них наиболее известным и проработанным является эхо-метод, который и используется в Работе 1. Обычно изучается стержень из исследуемого материала с отполированными торцами. На одном торце стержня помещается пьезоэлектрический преобразователь, подключенный к ВЧ-генератору, а на другом к ВЧ приемнику. Скорость звука в стержне определяется по времени задержки сигнала после двойного пробега, а величина поглощения звуковых волн – по ослаблению амплитуды сигнала. Таким образом, основным измеряемым фактором помимо толщины образца, является время пробега волн покристаллу.
К достоинствам этого метода следует отнести тот факт, что величины скорости и поглощения акустических волн измеряются "непосредственно", не требуя сложной обработки данных.
К недостаткам метода относятся высокие требования, предъявляемые к образцам и измерительной технике. На высоких частотах обеспечение приемлемого акустического контакта между преобразователем и образцом является сложной технологической задачей. В эксперименте необходимо проводить измерения по нескольким, а лучше по десятку эхо импульсов. Поглощение звуковых волн, возрастающее с частотой, при заданной чувствительности приемника ограничивает максимально возможные геометрические размеры образцов. В то же время уменьшение толщины образцов требует использования более коротких импульсов, что значительно повышает требования к импульсным системам на разрешение прибора по времени. При толщине образцов менее 1 мм удовлетворить эти требования очень трудно, практически невозможно. Было предложено использовать для измерения акустических потерь в веществе данные о добротности акустической резонаторной структуры, выполненной из исследуемого материала. Для измерения добротности необходимо измерить ширину полосы пропускания акустического резонатора. Таким образом основной измеряемой величиной становится не время, а частота.
Колеблющаяся пластинка как резонансная система
Рассмотрим колебания пластинки толщиной d, выполненной из изотропного материала. Будем считать, что идеально плоские грани пластинки идеально параллельны и перпендикулярны оси Х.
Уравнение упругих, например продольных или поперечных колебаний среды u(x,t), как известно из курса физики твердого тела, имеет вид:
Здесь ρ – плотность среды, с- модуль упругости.
Легко показать (самим), что при механически свободных границах,
Решение в случае гармонического решения с частотой ω:
имеет вид:
Видно, что при x=d апмлитуда колебаний становится максимальной. Частота, на которой это происходит равна:
, здесь n-целое число, равное числу полуволн, укладывающихся на толщине пластинки.
Если действовать с некоторой силой в нужной фазе с этой же частотой на одну или обе грани пластинки то возникнет резонанс – амплитуда колебаний пластинки будет бесконечно нарастать. При наличии же в среде затухания (потерь энергии) установится конечная амплитуда колебаний значение которой будет определяться равенством поступающей и затрачиваемой энергий за период колебания. В случае пьезоэлектрической среды, для пьезоактивного направления в кристалле можно записать уравнение:
Здесь Е – приложенное переменное электрическое поле, β – пьезомодуль для данного направления
-ужестченная, за счет пьезоэффекта, константа электромеханической связи, ε – диэлектрическая постоянная. В формуле учтено, что максимальная возбуждающая сила находится как раз на границах кристалла, где градиенты
максимальны
За счет пространственного разнесения возбуждающих сил кварцевая пластинка резонансно возбуждается только на частотах , соответствующих нечетным значениям n. При этом пластинка, включенная в электрическую цепь ведет себя как колебательный контур. Обычные (кварцевые) резонаторы работают на нечетных гармониках, причем номер гармоники редко превышает n = 3.
Реальные акустические потери, имеющиеся в пластинке, приводят к тому, что ширина полосы пропускания этого контура тем выше, чем больше потери. Связь между полосой пропускания эквивалентного электрического контура ∆ f и коэффициентом затухания в структуре потерями в структуре α как известно из радиотехники задается простой формулой:
Принцип резонансной спектроскопии
Для измерения акустических потерь и скорости звука в материалах на высоких частотах, как альтернатива эхо-методу, был предложен и разработан метод составного акустического резонатора.
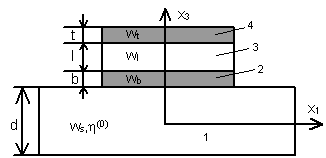
Структура составного акустического резонатора схематически показана на рис.1а, где исследуемый слой толщиной d, обозначен цифрой 1.
(а)
(б)
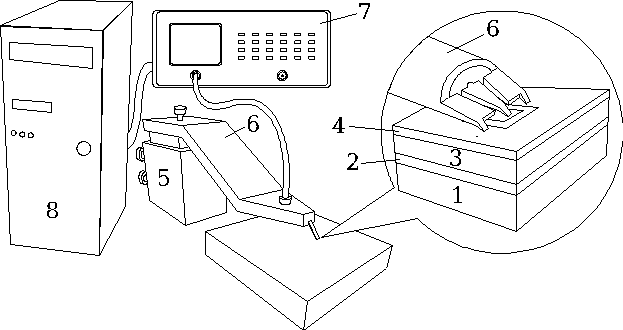
Рис.1. Схемы резонатора (а) и экспериментальной установки для измерений электрического импеданса или адмитанса составных акустических резонаторных структур (б); 1 - кристаллический слой, выполненный из материала с малыми акустическими потерями; 2 – электрод; 3 - пленка пьезоэлектрика; 4 - верхний электрод, 5 – микроподача, 6 – согласованный СВЧ-щуп, 7 – рефлектометр-анализатор цепей HP8753, 8 – компьютер.
На его поверхность нанесен электрод 2, выполненный, например, из алюминия - тонкая металлическая пленка толщиной b. Поверх этого слоя нанесена пленка пьезоэлектрика (например, окиси цинка) 3 толщиной l. Структура преобразователя или только верхний тонкопленочный металлический электрод 4 толщиной t, имеют сравнительно небольшие поперечные размеры, и именно под ними, по всей толщине структуры концентрируется колебательная энергия составного акустического резонатора. Суммарная толщина всех слоев преобразователя (2-4) порядка 1 мкм и много меньше, чем толщина исследуемого слоя – подложки 1, обычно составляющая от 0,5 мм до нескольких миллиметров. Таким образом, потери в слое во много раз превышают потери в преобразователе, что позволяет в дальнейшем ими пренебречь
Электроакустический преобразователь 2-4 , включенный во внешнюю электрическую цепь в составной резонаторной структуре, возбуждает и регистрирует акустические волны. Волны испытывают многократные отражения от свободных границ структуры. В случае, когда набег фазы акустической волны кратен целому числу π, амплитуды всех отраженных волн складываются в фазе, и формируется стоячая акустическая волна, т.е. возникает резонанс. Естественно, что при таком сложении величина суммарной амплитуды будет тем больше, чем меньше поглощение акустических волн в слоях при их распространении по структуре. Кроме того, она будет тем больше, чем больше отношение толщины слоя с малыми потерями к толщинам слоев преобразователя, в материалах которых потери выше.
Основные выводы теории составного резонатора
Строгая теория составного акустического резонатора, содержащего исследуемый слой, основывается на решении системы уравнений колебаний подобных уравнению (1) для каждого из слоев. Решения обычно ищут в виде суперпозиции волн, бегущих в каждом из слоев во взаимно-противоположных направлениях. Чтобы учесть затухание волн в слоях, волновые векторы берутся как комплексные величины. При этом реальная часть каждого волнового числа отвечает за волновой характер распространения деформации в слое, а мнимая часть отвечает за затухание. Далее полученный набор решений подставляется в граничные условия. В качестве граничных условий на границах между слоями выступают непрерывность механических смещений в слоях (неразрывность границы) и непрерывность механических напряжению. На свободных границах механические напряжения приравнивались нулю (условие свободных границ). Электрическое напряжение между электродами, возникающее вследствие пьезоэффекта, в результате оказывалось возможным записать через независящее от координаты внутри преобразователя переменное электрическое поле. Через это же поле выражался и протекающий ток. После деления напряжения на ток оказалось возможным получить достаточно громоздкое выражение для входного электрического импеданса структуры Ze. Формула для электрического импеданса связывает электрические характеристики структуры в зависимости от частоты итолщин и акустических характеристик всех слоев входящих в структуру.
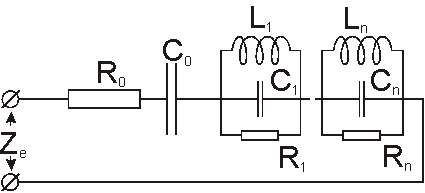
Электрические эквивалентные схемы составной резонаторной структуры
Формулу для входного импеданса составной резонаторной структуры наиболее удобно представить в виде ряда:
Где С0 – емкость между электродами преобразователя,
,
Здесь
- квадрат константы электромеханической связи,
,
, b0 и q0 – соответственно действительные части волновых векторов в слоях, соответственно, пьезоэлектрика и исследуемого материала, l и d - толщины этих слоев.
Члены ряда (2) могут быть выражены через параметры эквивалентной схемы, которые являются функциями акустических характеристик слоев и их геометрических размеров. Каждая из компонент под знаком суммы соответствует параллельному резонансу на частоте w = wn.
,
Рис.2. Эквивалентные схемы для определения добротности на частотах антирезонансов (а) и резонансов (б) составного резонатора.
Эквивалентная схема составной резонаторной структуры (Pис.2) состоит из последовательных сопротивления и емкости, а также серии параллельных LCR контуров, каждый из которых соответствует одному из параллельных резонансов структуры. Вместе с емкостью C0 каждый LCR контур вызывает n –й последовательный резонанс.
Вывод:
Составная резонаторная структура имеет большое число резонансов и связанных с ними антирезонансов расположенных в широком диапазоне частот (обычно сотни МГц-несколко ГГц). Расстояние между резонансами и антирезонансами в частотной области относительно невелико - в зависимости от толщины слоев обычно 1…10МГц.
Таким образом, измеряя на одном образце в широком диапазоне частот ширины резонансных линий , можно получить данные о частотной зависимости коэффициента поглощения акустических волн.
Процедура измерения добротности составного акустического резонатора
Измерение добротности составного акустического резонатора производят путем включения его в тракт СВЧ-рефлектометра (см. Pис.1б), позволяющего измерить комплексный коэффициент отражения электромагнитной волны от резонаторной структуры S11 в зависимости от частоты. Современные рефлектометры позволяют производить измерения частотных характеристик S11 с высоким разрешением по частоте (до единиц герц в гигагерцовом диапазоне) и записывать результаты измерений действительной и мнимой частей S11 либо в собственную память, либо в память компьютера, соединенного с рефлектометром. В зависимости от того, на каком варианте эквивалентной схемы будет базироваться последующий анализ при помощи внутреннего процессора прибора или внешнего компьютера данные пересчитывают в действительную и мнимую части электрического импеданса или адмитанса. Отметим, что этот анализ основан на математической обработке полученного экспериментально массива данных об S11(f). Целью анализа является определение ширины полосы пропускания
колебательного контура, соответствующего данному резонансу или антирезонансу на частоте fn. Зная ширину полосы пропускания, можно найти добротность резонатора
по формуле
Добротность резонатора можно также найти по углу наклона
фазо-частотной характеристики резонатора
в точке резонанса (
численно равен
)
Соответственно коэффициент поглощения в материале резонатора можно определить по вышеприведенной простой формуле
Процедура измерения полосы пропускания акустического резонатора cвязана с его включением в тракт СВЧ - рефлектометра позволяющего измерить комплексный коэффициент отражения электромагнитной волны от резонаторной структуры S11 в зависимости от частоты.
Анализ формулы для коэффициента отражения совместно с выражениями для входного электрического импеданса, соответствующего эквивалентным схемам, приведенным на рис.1, показал, что при некоторых соотношениях между волновым сопротивлением тракта и омическим сопротивлением в эквивалентной схеме, на кривой зависимости фазы коэффициента отражения S11 от частоты появляются экстремумы. Измеренное расстояние между этими экстремумами в частотной области дает возможность найти ширину полосы пропускания.
В частности, для частоты вблизи резонанса с номером n (эквивалентная схема Рис.2) входной электрический импеданс равен:
Подставляя это выражение в формулу для коэффициента отражения:
,
находим частоты, соответствующие экстремумам фазы в окрестности данного резонанса
и
а затем и разность между ними
. Далее, поделив на эту разность частоту резонанса, имея в виду, что
, получим:
Таким образом, в случае
<<1, найденное значение
соответствует с хорошей точностью полосе пропускания последовательного колебательного контура на частоте n- го резонанса. Как известно из радиотехники, полосу пропускания колебательного контура можно найти из частотных характеристик, отмечая граничные частоты, по уровню
от максимума модуля проводимости для последовательного колебательного контура или максимума сопротивления для параллельного контура. Другой способ определения полосы пропускания связан, как указывалось, с нахождением крутизны фазово-частотной характеристики в точке резонанса. Можно также измерить полосу пропускания резонатора по фазово-частотной характеристике электрического импеданса как разность между частотами, соответствующими сдвигу фаз ±45° от фазы в точке резонанса. Кроме того в указанных выше условиях измерение добротности резонатора сводится к простому измерению разности частот экстремумов
на фазово-частотной характеристике коэффициента отражения электромагнитной волны от резонатора и простому вычислению по формуле (6).
В более общем случае можно показать, что в составном акустическом резонаторе, связь между разностью
между частотами антирезонанса
и резонанса
имеет вид:
где
- частота, при которой на длине структуры укладывается целое число n длин акустических волн,
- квадрат эффективной константы электромеханической связи, величина которой обратно пропорциональна номеру гармоники, Qn- добротность резонатора. У составных резонаторов СВЧ диапазона номера гармоник велики – сотни и даже тысячи. Поэтому с ростом n разность
между частотами антирезонанса
и резонанса
стремится к пределу:
Разность
между частотами антирезонанса и резонанса может быть измерена непосредственно на частотной зависимости модуля импеданса. С этой разностью совпадает в этом случае и разность между частотами экстремумов на фазовой характеристике коэффициента отражения
.
Таким образом, процедура измерения добротности и коэффициента поглощения также оказывается очень простой.
Примеры
Описанные процедуры проиллюстрированы ниже на примерах измерения добротности низкочастотного кварцевого резонатора и составного резонатора на объемных продольных волнах со структурой Al– ZnO - Al – пластина ИАГ. Измерения фазы коэффициента поглощения проводились при помощи рефлектометра-анализатора цепей. Ниже рассмотрены случаи измерения добротности эквивалентных колебательных контуров в области резонансов и антирезонансов.
Измерения добротности на частоте резонанса
Проводились измерения добротности резонансного пика стандартного серийного резонатора, работающего на третьей гармонике, на частоте около 9 МГц.
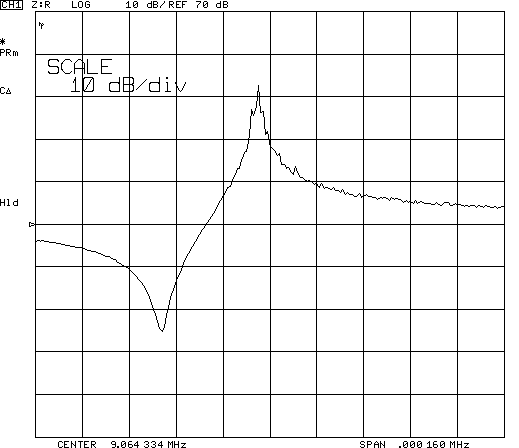
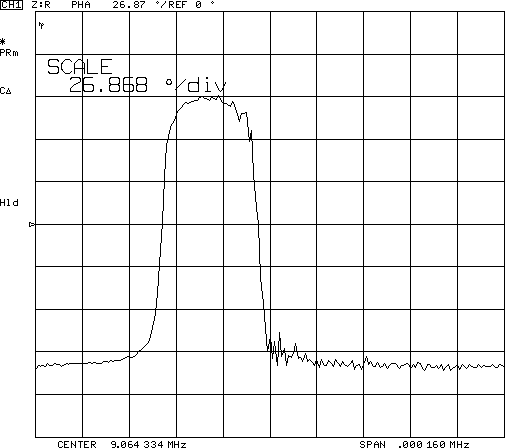
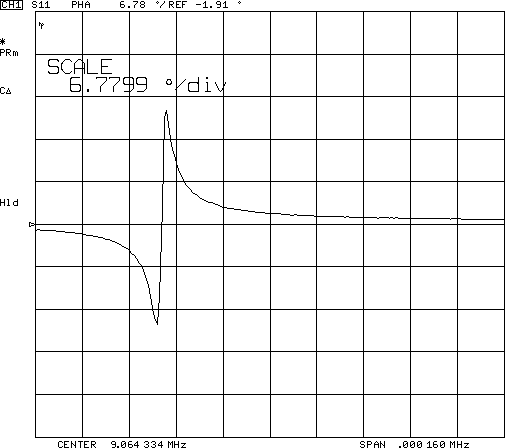
Частотные характеристики амплитуды и фазы электрического импеданса, а также фазы коэффициента отражения, представлены, соответственно, на Pис.3а, 3б. 3в. На рис 3.а хорошо видны области резонанса и антирезонанса.
Рис.3.а Частотная характеристика амплитуды электрического импеданса высокодобротного резонатора
Рис.3.б Частотная характеристика фазы электрического импеданса
Рис.3в. Частотные характеристики фазы коэффициента отражения электромагнитной волны от резонатора.
Из сравнения данных представленных на Рис.3 видно, что точки экстремума фазы коэффициента отражения действительно соответствуют области резонанса.
Для проведения измерений параметров высокодобротного резонатора с высокой точностью необходимо высокое частотное разрешение. Соответствующие частотные характеристики фазы коэффициента отражения, амплитуды и фазы электрического импеданса представлены, соответственно, на Pис.3.
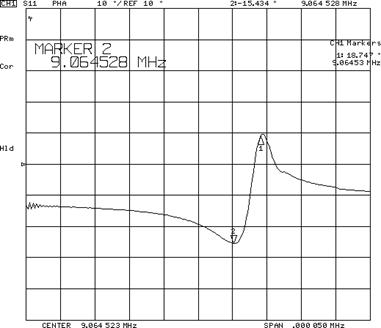
Рис.4 Частотные характеристики фазы коэффициента отражения. Цена деления 5 Гц.
Из данных, представленные на рис.4 получено значение полосы пропускания
f = 3,85 Гц. Из данных, рис.4 легко непосредственно измеряются частота резонанса f = 9064531Гц и величина последовательного сопротивления r3= 185,6 Ом .
Сопротивление тракта равно
= 50 Ом и таким образом
=0,27 <1 и для нахождения добротности можно использовать формулу (6). Полученное значение добротности Q =2,22 106. Как указывалось, добротность можно найти, измерив полосу пропускания резонатора как разность между частотами, соответствующими сдвигу фаз ±45° от фазы в точке резонанса. Найденное значение добротности равно 2,3 106
Таким образом, найденные двумя способами, значения добротности отличаются на 3% и практически совпадают.
Вычисленные по формуле (1) значение коэффициента поглощения совпадает с табличными данными для данного среза кристалла кварца.
Измерения добротности на высоких гармониках составных акустических резонаторов
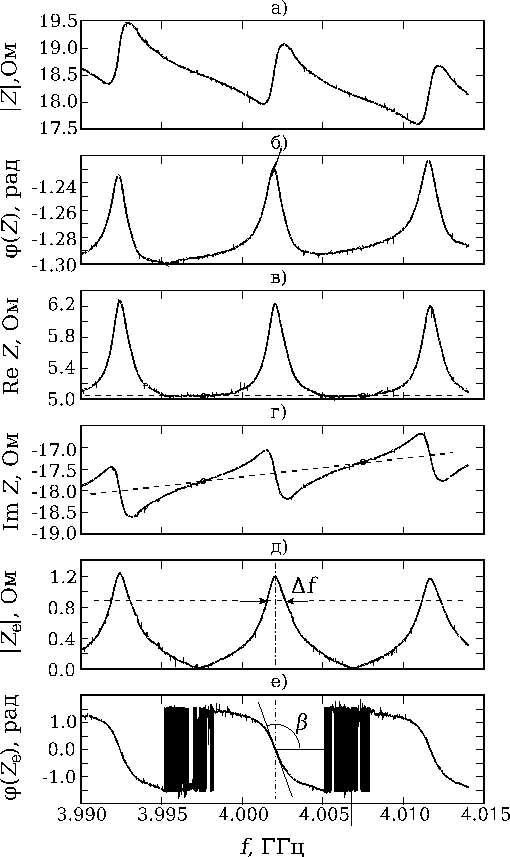
В качестве примера ниже на рис.5 показаны частотные зависимости амплитуды (а) и фазы импеданса (б), действительной (в) и мнимой (г) частей импеданса. Эти экспериментальные данные получены для структуры Al-ZnO-Al- пластина ИАГ.
Для того чтобы исключить влияние емкости между электродами резонатора, т.е. последовательной емкости в эквивалентной схеме, а также паразитного сопротивления была проделана следующая процедура. Из величин полных мнимой ImZ и действительной ReZ частей импеданса (Pис.4в, 4г) были вычтены значения этих величин, соответствующие их уровню вне резонансов. В результате получены данные для комплексного импеданса (ImZe и ReZe) только для параллельных эквивалентных колебательных контуров в схеме, приведенной на Pис.2. Этим параллельным контурам соответствуют антирезонансы на Pис.5а. Далее эти данные использованы для нахождения модуля
и фазы
импеданса в зависимости от частоты (Pис.5д и Pис.5е). На Рис.5д показана процедура нахождения по данным эксперимента ширины полосы пропускания параллельного контура по уровню
амплитудной характеристики, а на Рис.5е – аналогичная процедура для нахождения крутизны фазовой характеристик. Оказалось, что значения добротности (Q = 3173 и Q = 3157), вычисленные по формулам (3), (4) с использованием полученных данных, практически совпадают.
Устранение последовательной емкости приводит к небольшому уменьшению частоты результирующего резонансного пика, но при этом, как можно показать, его добротность остается неизменной. Простой способ определения добротности с использованием формулы (7а) дает соответственно значения 3165.
Видно, что во всех случаях измеряемая ширина полосы пропускания и, следовательно добротность, практически одни и те же. Заметим, что относительно низкая добротность связана с неполным захватом энергии колебаний на этой частоте.
Вычисленные значения коэффициентов поглощения превышают более чем втрое табличные данные. В данном случае объяснение расхождения связано с большими потерями энергии, обусловленными рассеянием акустических волн слишком большими шероховатостями поверхности, наличие которых было установлено измерениями с помощью атомного силового микроскопа.
Таким образом, описанная простая процедура позволяет находить с достаточной точностью значения добротности пьезоэлектрических и многочастотных составных акустических резонаторов во многих практически важных случаях.
При использовании метода резонансной акустической спектроскопии для измерения затухания акустических волн, следует иметь в виду, что рассмотренная выше модель составного акустического резонатора учитывает полные потери энергии. В них вносят вклад: взаимодействие акустических волн с тепловыми фононами, уходом энергии из-под электродов преобразователя, возбуждение пластиночных мод в структуре, дифракция на апертуре преобразователя и рассеяние акустических волн шероховатостями поверхности. Для нахождения затухания из-за взаимодействия с фононами необходимо свести к минимуму потери за счет других механизмов. Так, на некоторых частотах и при определенных соотношениях между толщинами пластины и слоев преобразователя возможен полный захват энергии колебаний в резонаторной области и этот вид потерь исключается [8]. Дифракционные потери можно резко уменьшить, увеличивая апертуру преобразователя. Потери на шероховатостях поверхности можно снизить улучшением качества полировки, а их вклад в общее затухание тем меньше, чем толще исследуемый образец.
Рис.5. Полученные из экспериментальных данных частотные зависимости: амплитуды (а) и фазы импеданса (б), действительной (в) и мнимой (г) частей импеданса, амплитуды (д) и фазы (е) импеданса эквивалентных параллельных контуров.
Для нахождения величины поглощения в пластине подложки необходимо вычесть из общих потерь вклад, связанный с потерями в слоях преобразователя. Величину этого вклада можно оценить из табличных данных о коэффициенте поглощения в слоях преобразователя и измеренных независимо толщин слоев. В случае толстой подложки этими потерями обычно можно пренебречь.
Контрольные вопросы
1. В чем состоит принцип резонансной акустической спектроскопии ?
2. Опишите структуру составного резонатора и роль каждого из слоев.
3. Как связаны акустическая добротность с потерями в структуре и коэффициентом поглощения?
4. Назовите методы определения ширины полосы пропускания электрического колебательного контура эквивалентного составной резонаторной структуре.
5. В чем достоинства и недостатки метода составного акустического резонатора.
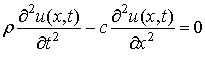
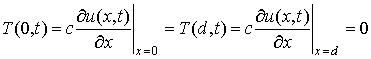
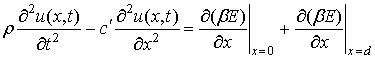
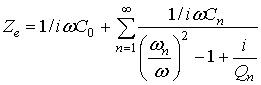
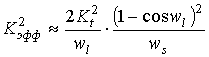
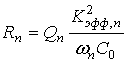
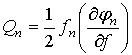
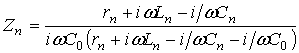
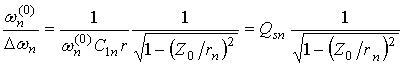
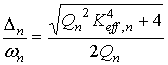 (7)
(7)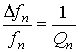 (7
(7